Multi-dimensional addressing with tensors

Let’s begin with understanding why we’d want to map memory in the first place. At the end of the day, memory is a linear object. We have the first address, and the address after that, and so on. So what do we do when we want to interpret the data in that memory in nonlinear fashion?

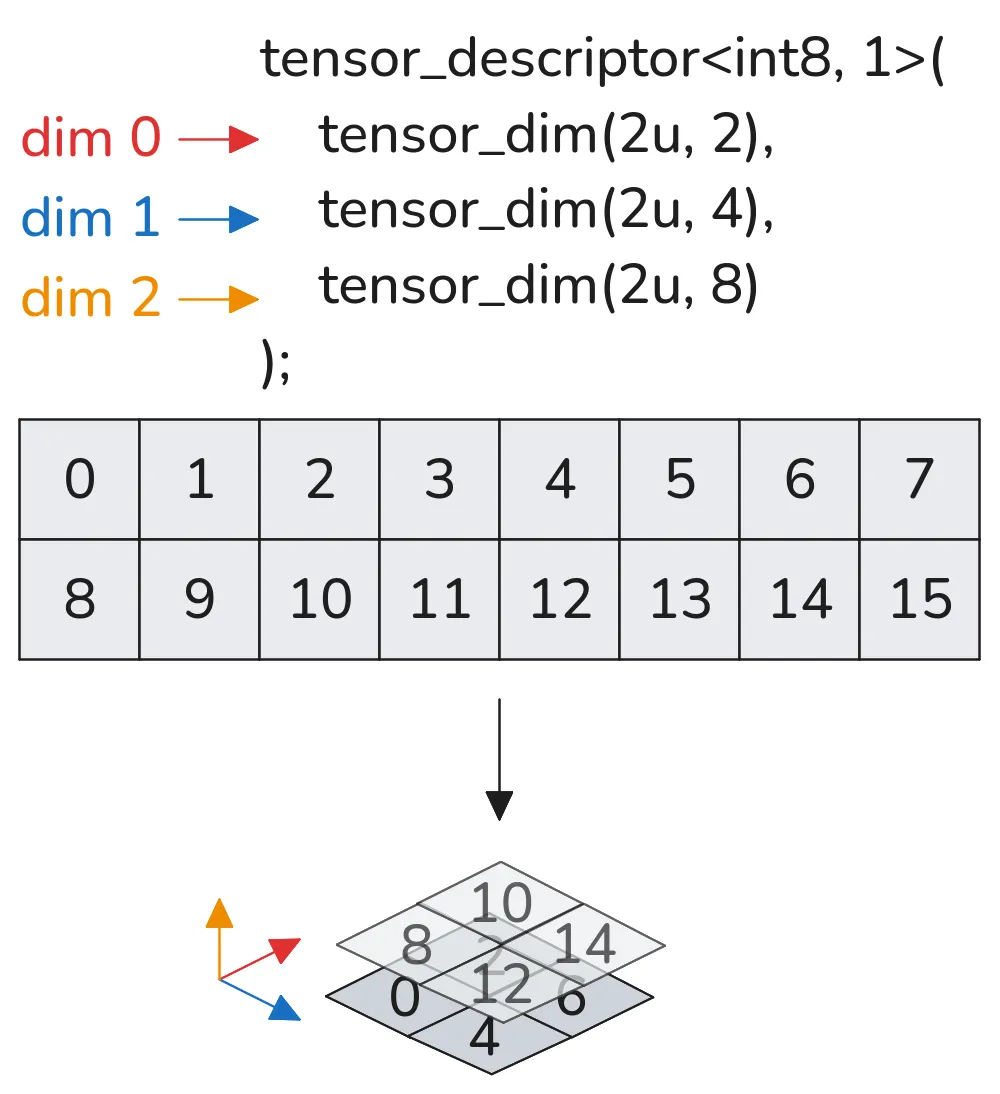
Consider the following vector: [A0, A1, A2, A3], if we jump twice from the starting position, and then increment it we process it as A0 → A2 → A1 → A3. At the core of this is the idea of a dimension:

tensor_dim(unsigned num, int step)

Clearly we need to know how far we need to jump, the step size, but we also need to know when to change the starting position, that’s num, which corresponds to how many elements in the dimension. With this defined, it’s easy to make a tensor:

But how do we actually get the data from memory? The whole purpose of this tensor_descriptor abstraction is so that we can stop worrying about iteration or pointer arithmetic and just get the data out in some ordered manner. The API provides this as a stream:

make_buffer_stream(T* base, const TensorDescriptor &tensor_d)

This makes a stream of elements from a buffer, organized in the dimensions of the tensor. This stream works similarly to iostream, elements can be plucked from the stream by the overloaded >> operator, or a pop() function. Similarly, pushed into a stream with << or push().

Because we’re talking about a vector processor here, a tensor dimension “unit” does not necessarily have to be a single element, it can be a whole vector on its own. Consider the following tensor:

tensor_descriptor<int8, 32>
(
    tensor_dim(2u, 1),
    tensor_dim(2u, 2),
    tensor_dim(2u, 4)
)

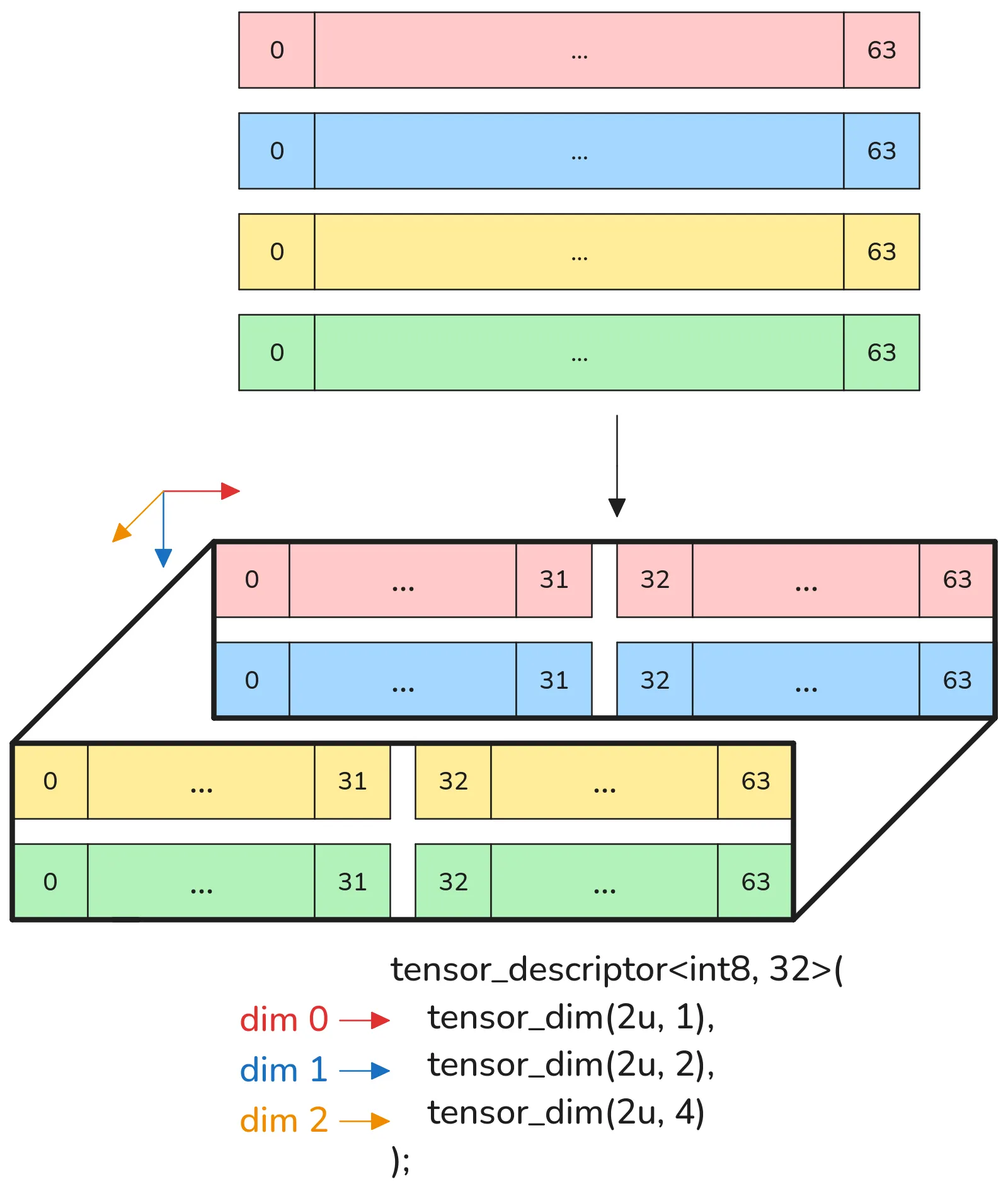
Notice that we end up needing a minimum of 4 vectors to make this tensor, which translates to 256 elements. This is what the buffer in buffer stream means, each element of our stream is part of some buffer, and it’s being streamed out following the tensor description:

alignas(vec_decl_align) static int16 buff[256];

std::iota(buff, buff + 256, 0);

auto desc = tensor_descriptor<int8, 32> (
    tensor_dim(2u, 1),
    tensor_dim(2u, 2),
    tensor_dim(2u, 4)
);

int8* ptr = buff;

auto tbs = make_buffer_stream(ptr, desc);

for (int i = 0; i < 8; i++)
{
    vector<int8, 32> v;
    tbs >> v;
    // equivalent:
    //   auto v = tbs.pop();
}

The output of the stream is as you’d expect. It advances by the steps of dimension 0. When it has advanced by the size of the dimension, it advances to the next dimension, upon which it wraps back to the lowest dimension increments. These offsets can all be calculated from a base pointer (ptr).

So the stream is: A[0,0,0] → A[1,0,0] → A[0,1,0] → A[1,1,0] → A[0,0,1] → A[1,0,1] → A[0,1,1] → A[1,1,1]

And because we populated the buffer with std::iota, this is just the numbers 0 — 255 (in intervals of 32).

An important nuance of the buffer streams is that they’re defined recursively. An N-dimensional tensor decomposes into ⌊(N-1)/3⌋ nested streams with a final N % 3 leaf stream. In these cases the .pop() operation returns the innermost stream and advances the outer stream. Let’s look at this:

auto desc = tensor_descriptor<int8, 32>(
    tensor_dim(2u, 1),  // dim 1
    tensor_dim(6u, 4),  // dim 2
    tensor_dim(2u, 0),  // dim 3
    tensor_dim(2u, 2)   // dim 4
);

Now how does this 4-dimensional tensor get streamed? We know the first .pop() call will return a single (4 % 3) leaf stream corresponding to dim 1, and dim 2 is advanced. This stream essentially looks like:

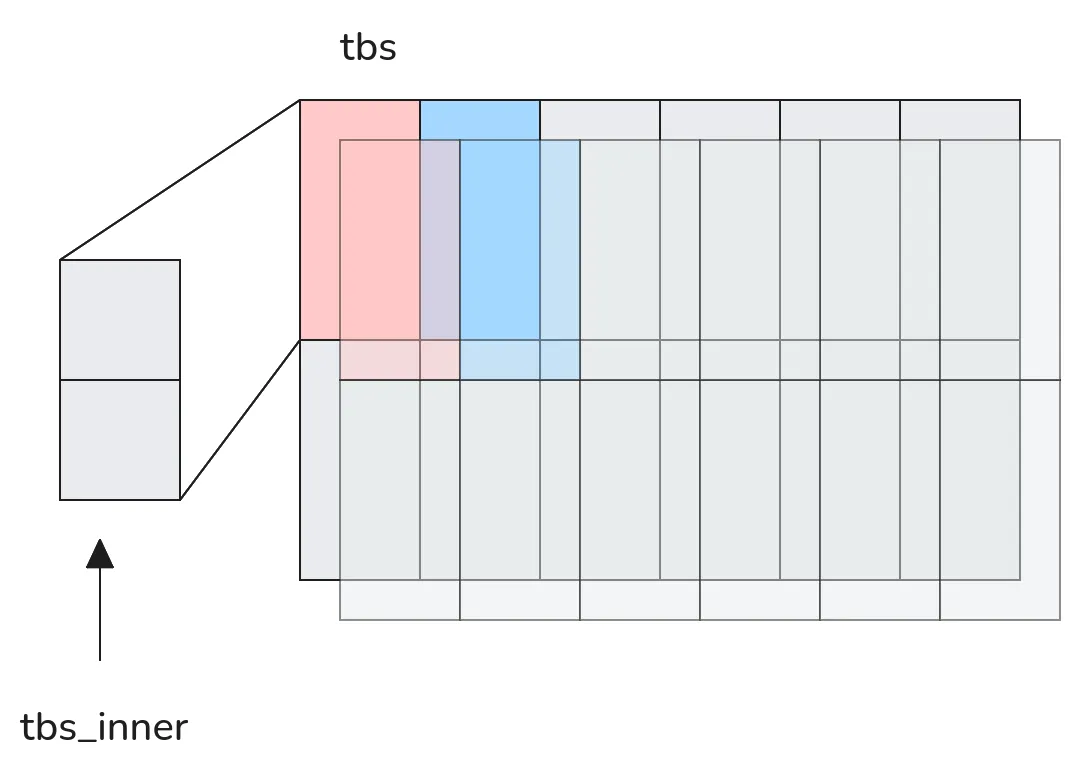
This highlights another useful property of these tensor_descriptors, notice that dim 3 has a step size of 0, which means it simply repeats the data to “fill out” that dimension, since it needs 2u elements. You could think of dimensions 2 — 4 to map out a 3-dimensional tensor while dimension 1 “pops” out each time.

A tricky part is that dim 4 has a step size of 2. This is related to that nifty step-less dimension 3, since it doesn’t actually “offset” our memory in any way, the next dimension is calculated following from it. I try to visualize it like this:

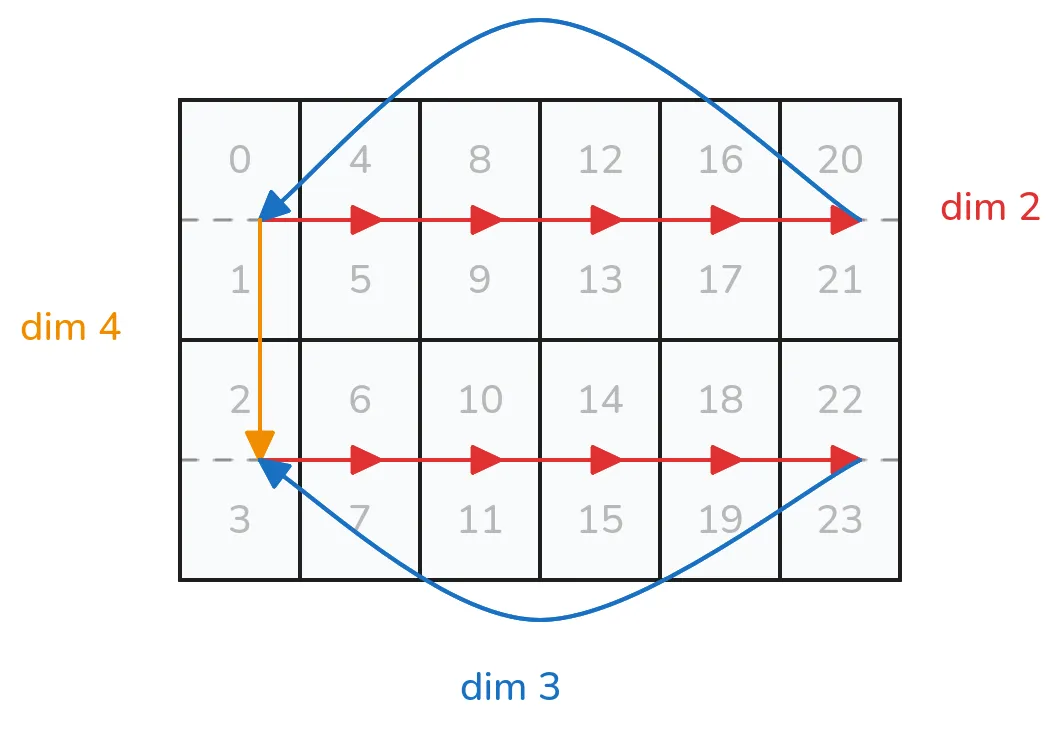
Considering that the inner leaf stream is popped here. Then once dim 3 sends you back the jump is from 0 to 2, while the data itself flows from 21 to 2. The code for this is:

auto tbs = tensor_buffer_stream(ptr, desc);

for (unsigned i = 0; i < 6 * 2 * 2; ++i)
{
    auto tbs_inner = tbs.pop(); // returns inner leaf stream

    vector<int8, 32> one, two;
    tbs_inner >> one >> two;
}

This abstraction is useful when writing GEMM kernels, which I plan on talking about sometime soon.

gabriel!

Multi-dimensional addressing with tensors